Overview

This was a cool throwback to 61b, looking intently at data structures and working with a kind of large codebase. Implementing Casteljau's algo was pretty straightforward. But when it came to half-edges, pictures were definitely necessary. This was a real blessing.

Section I: Bezier Curves and Surfaces

Part 1: Bezier curves with 1D de Casteljau subdivision

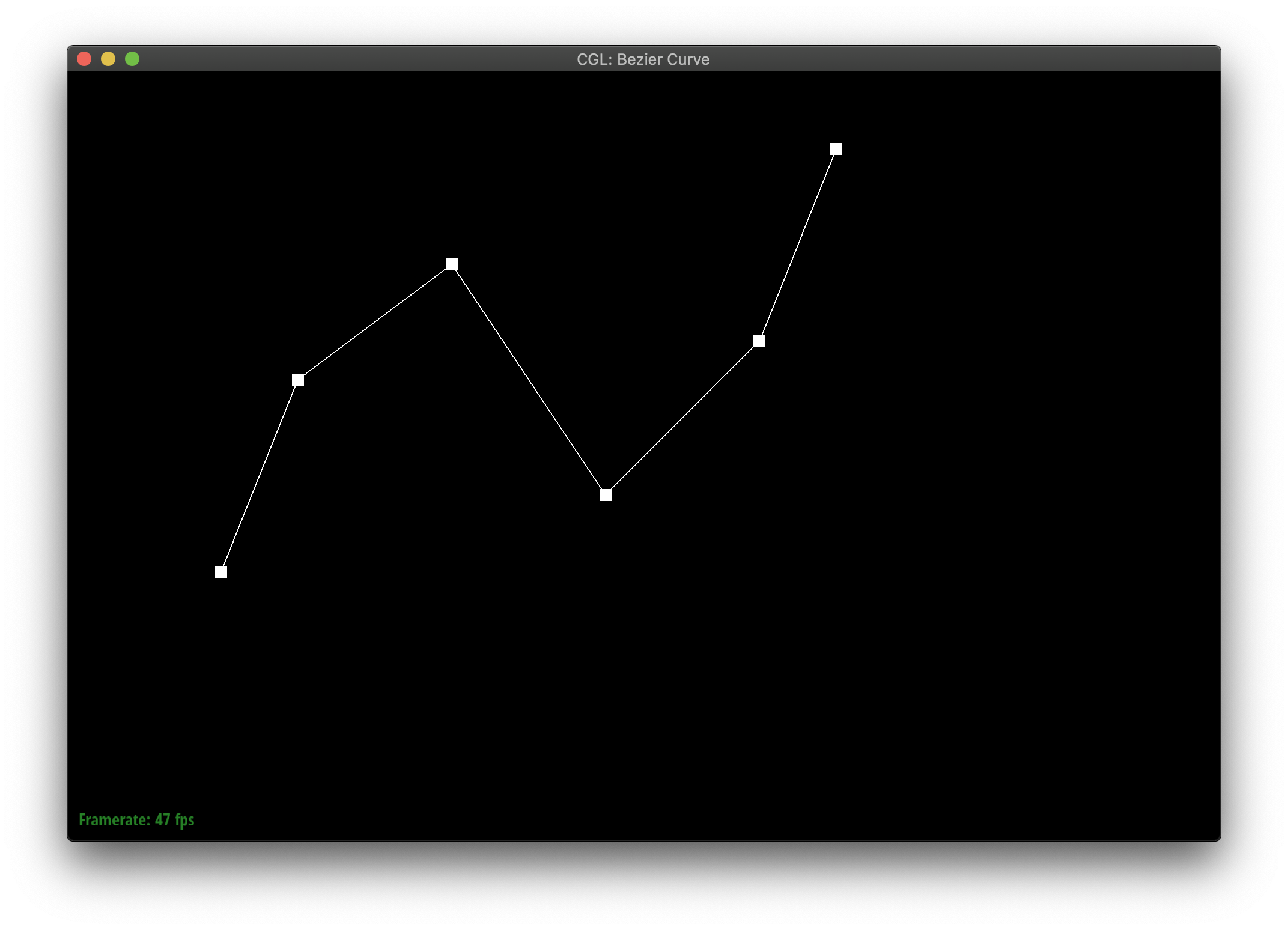
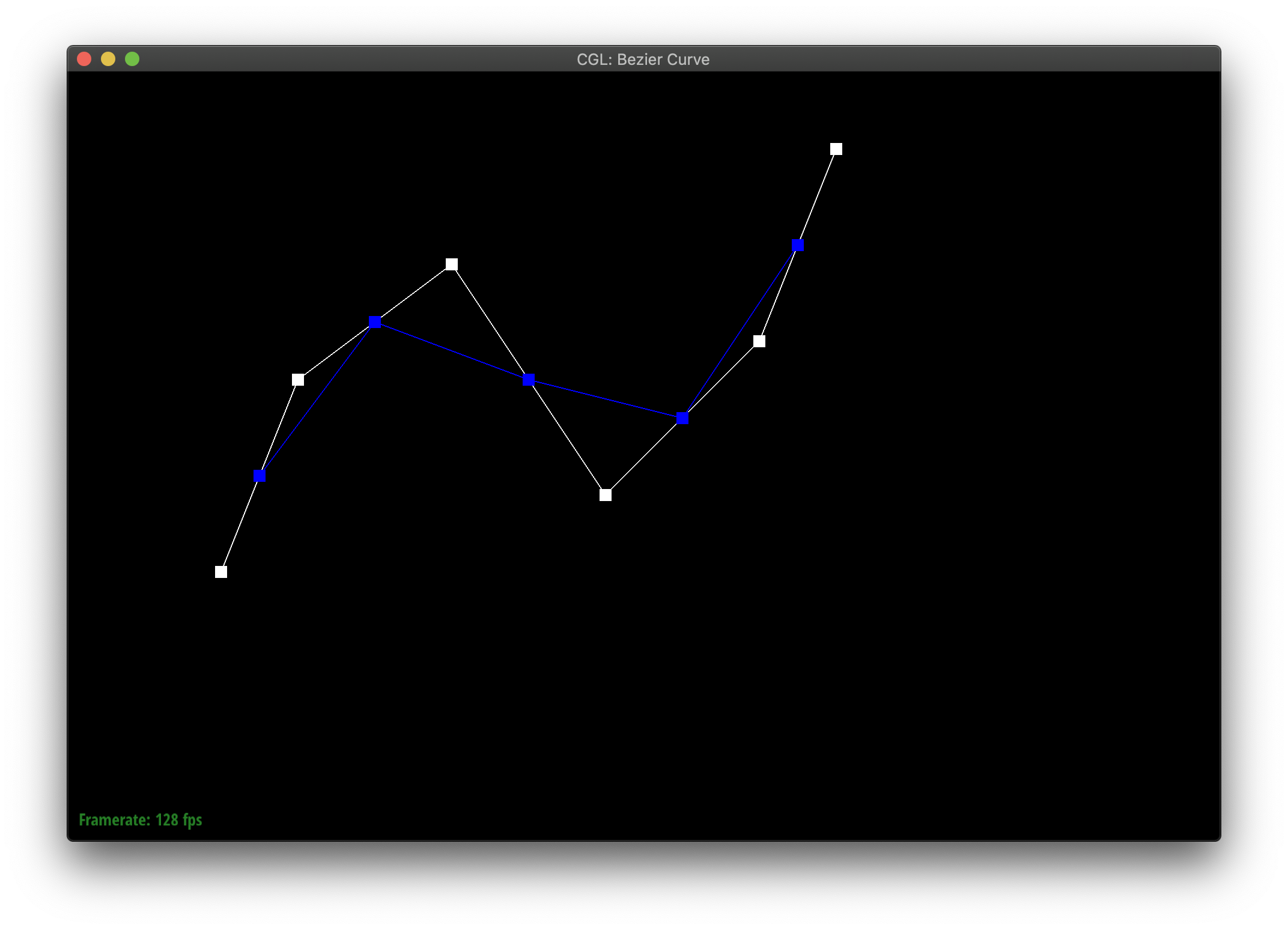
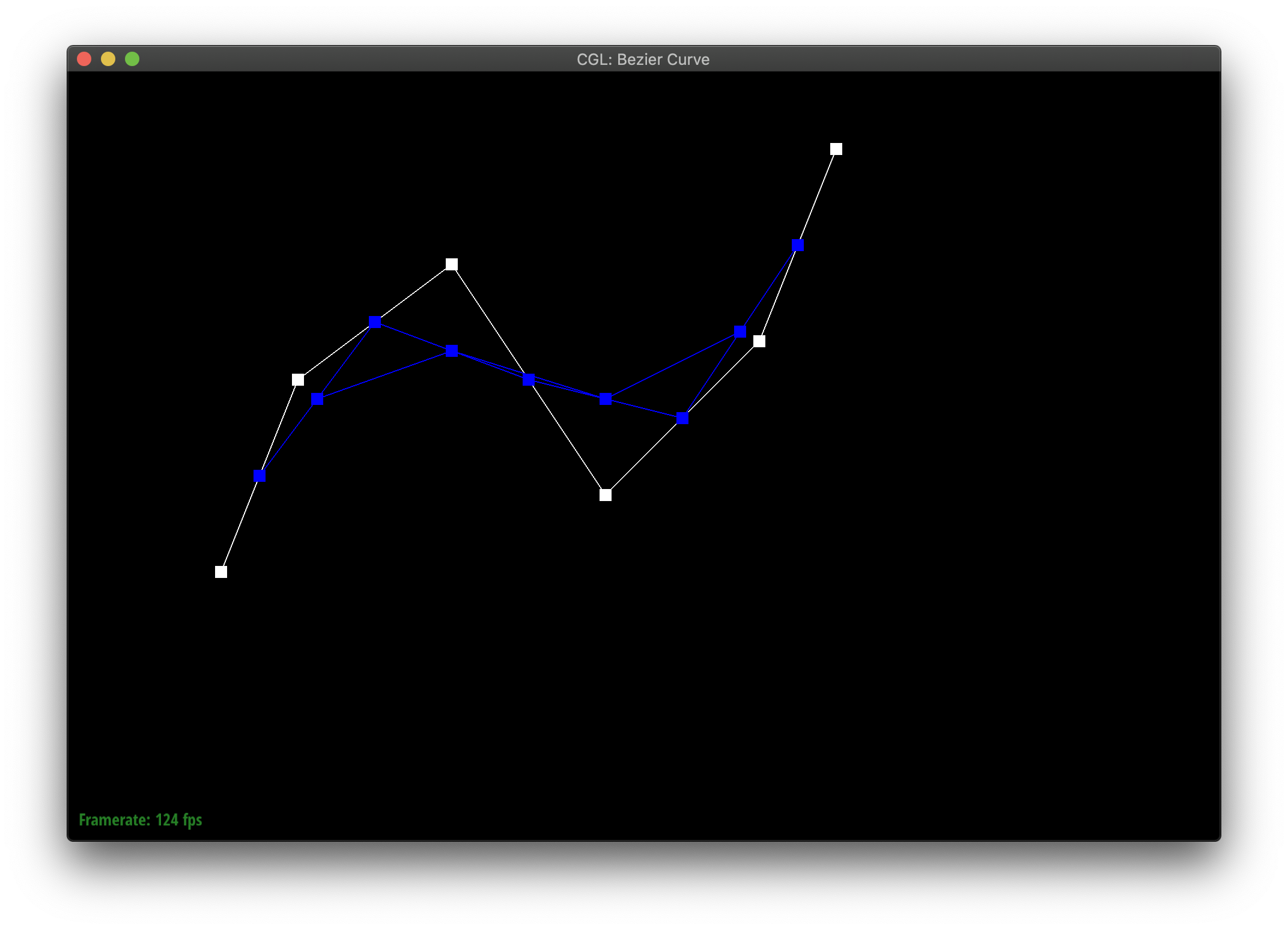
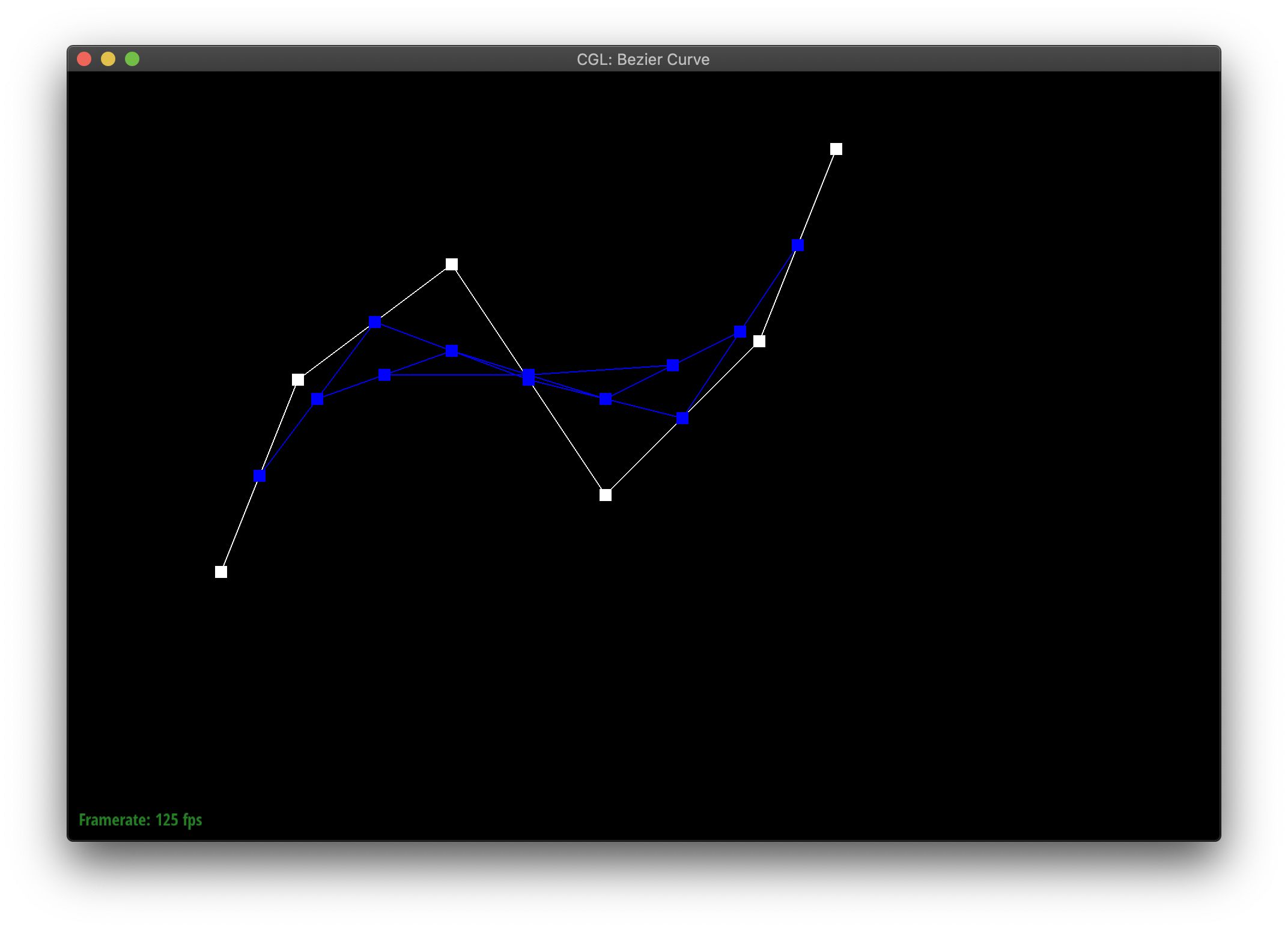
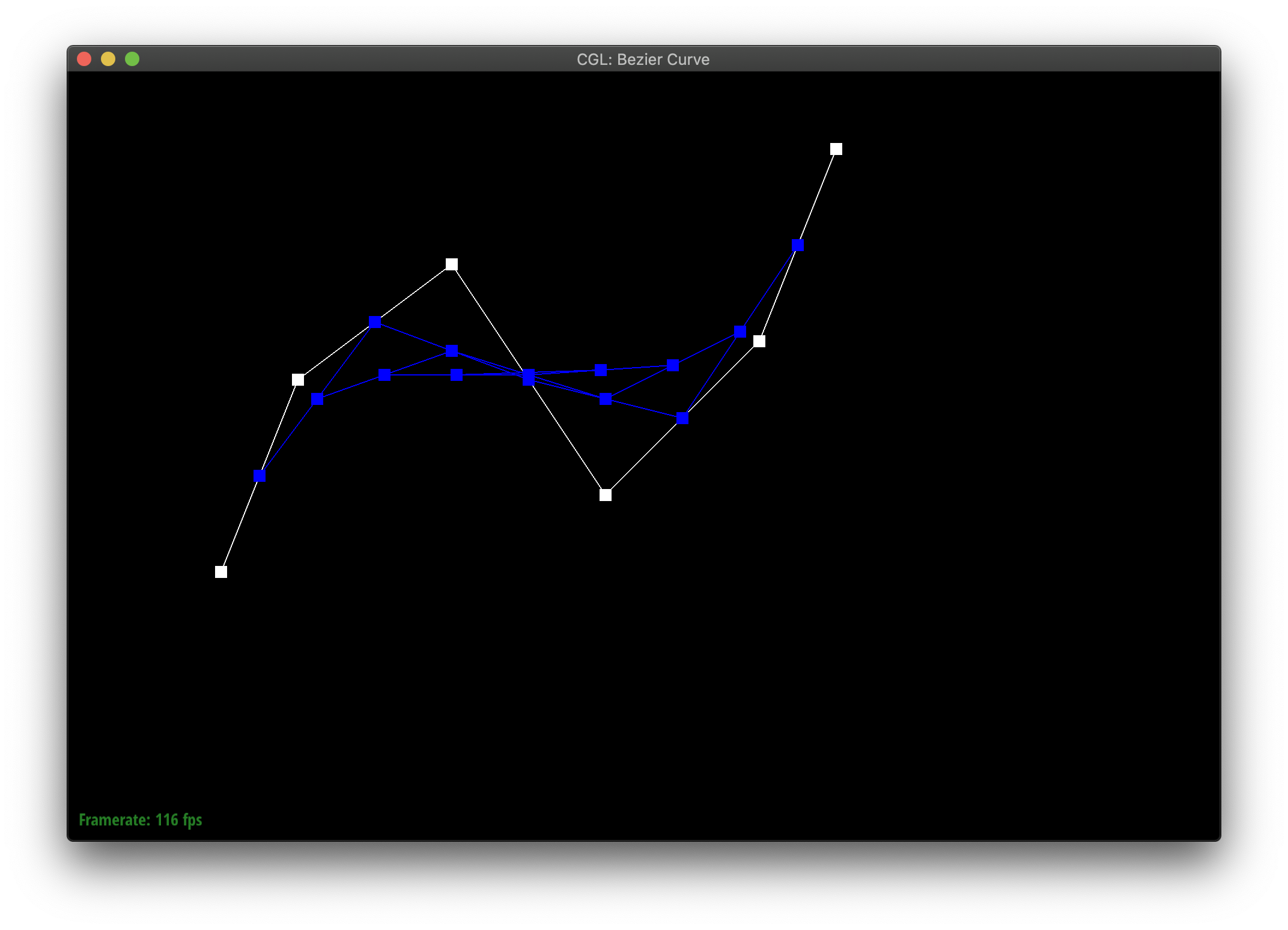
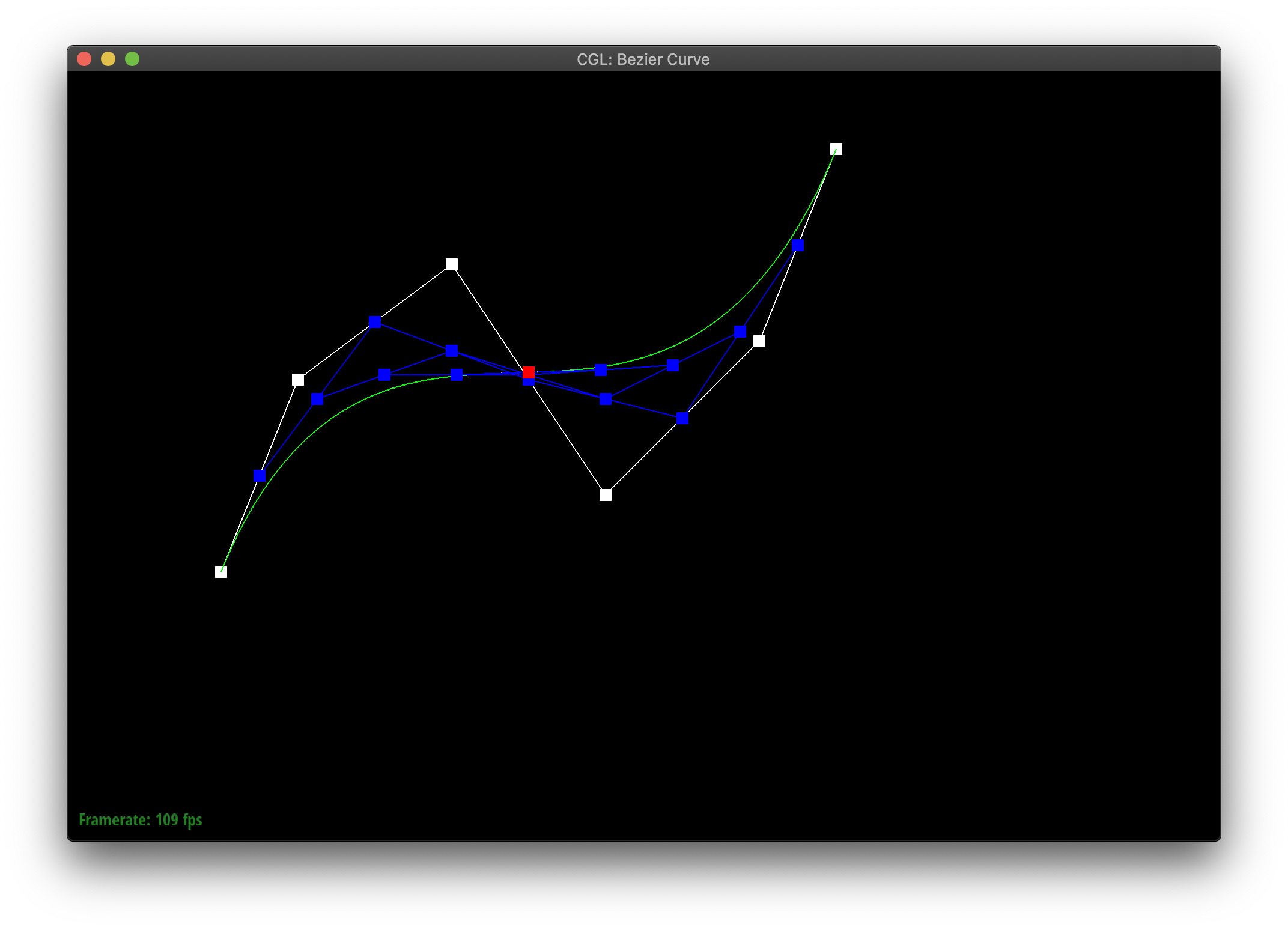
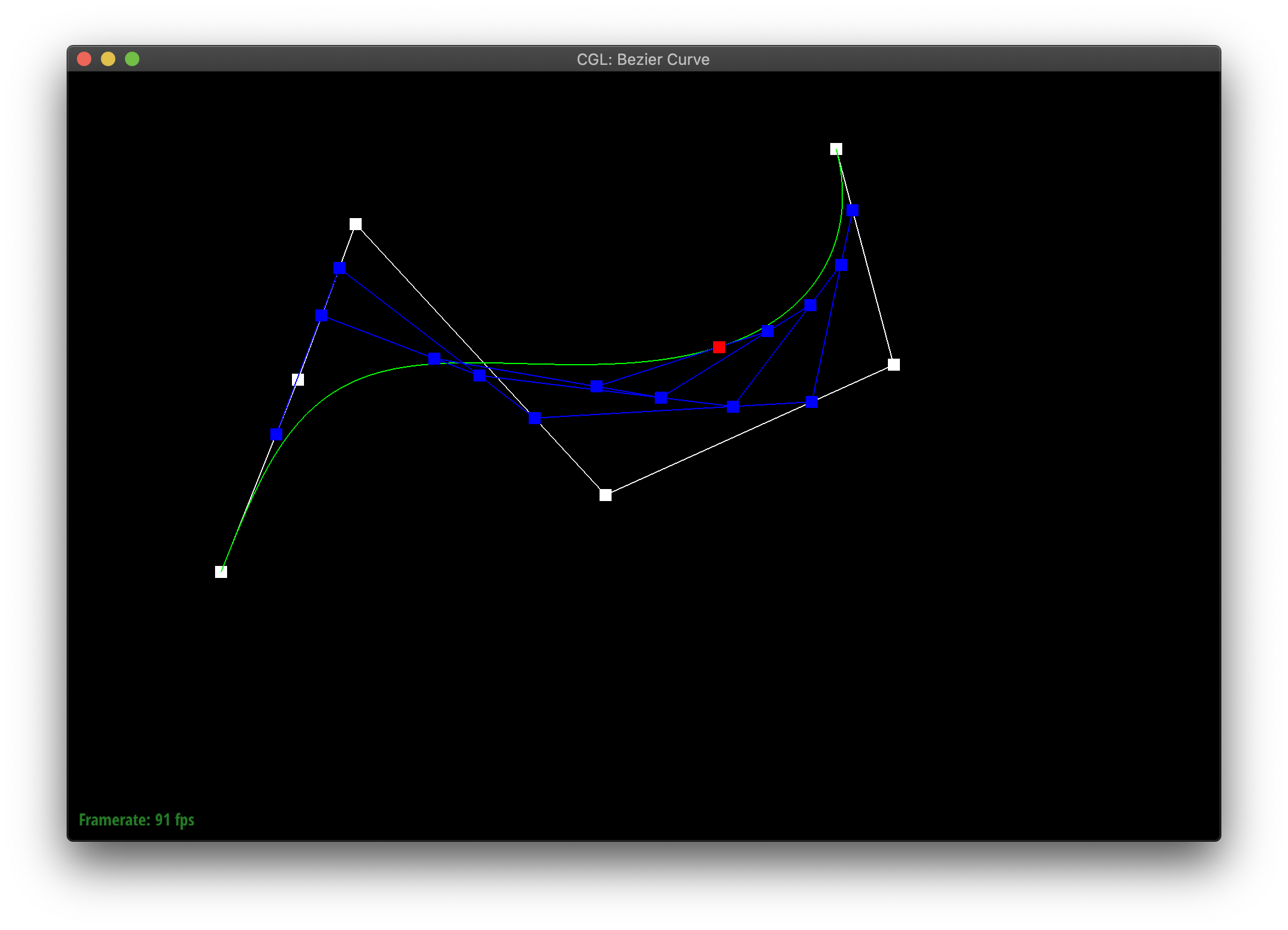
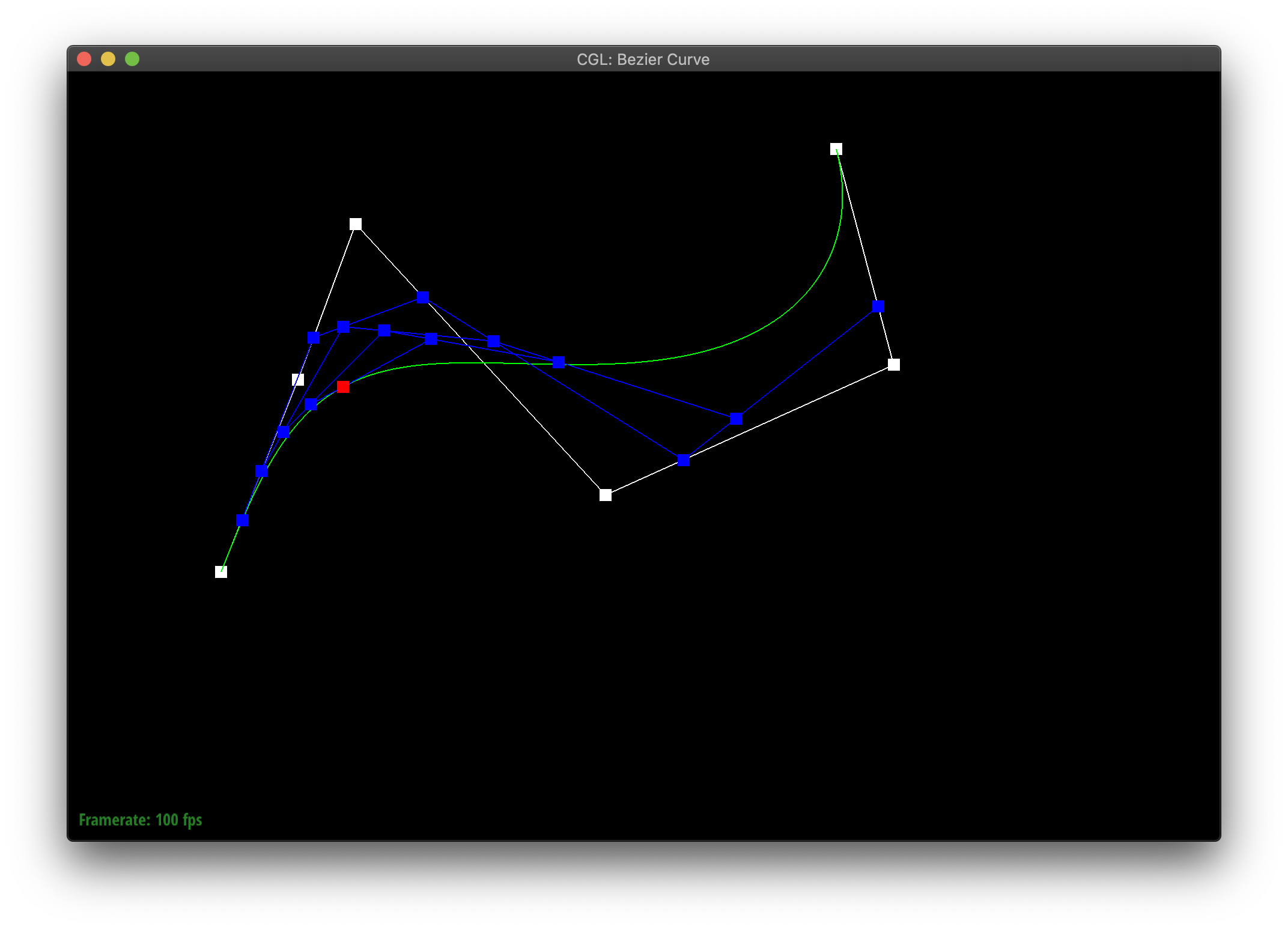
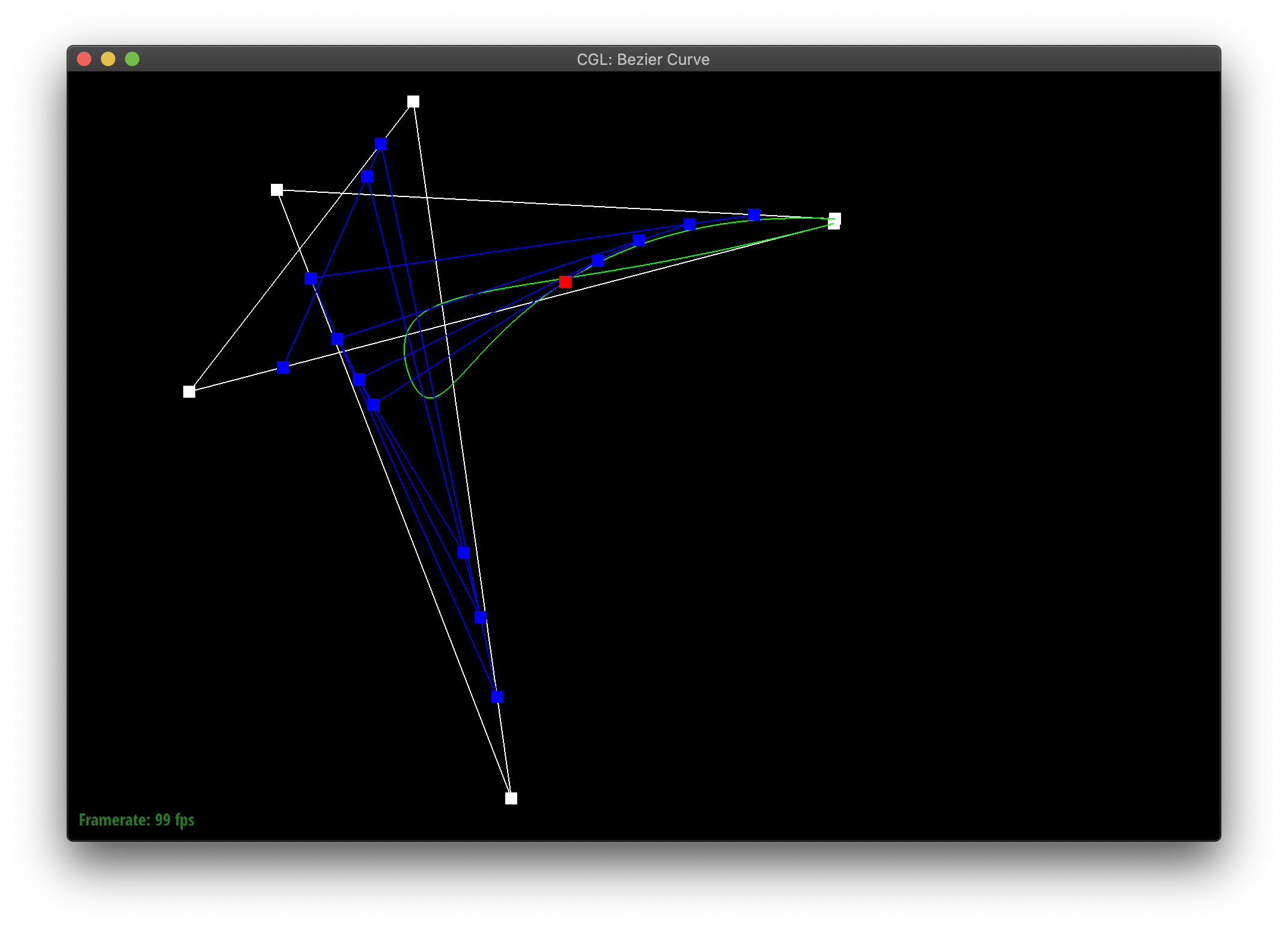
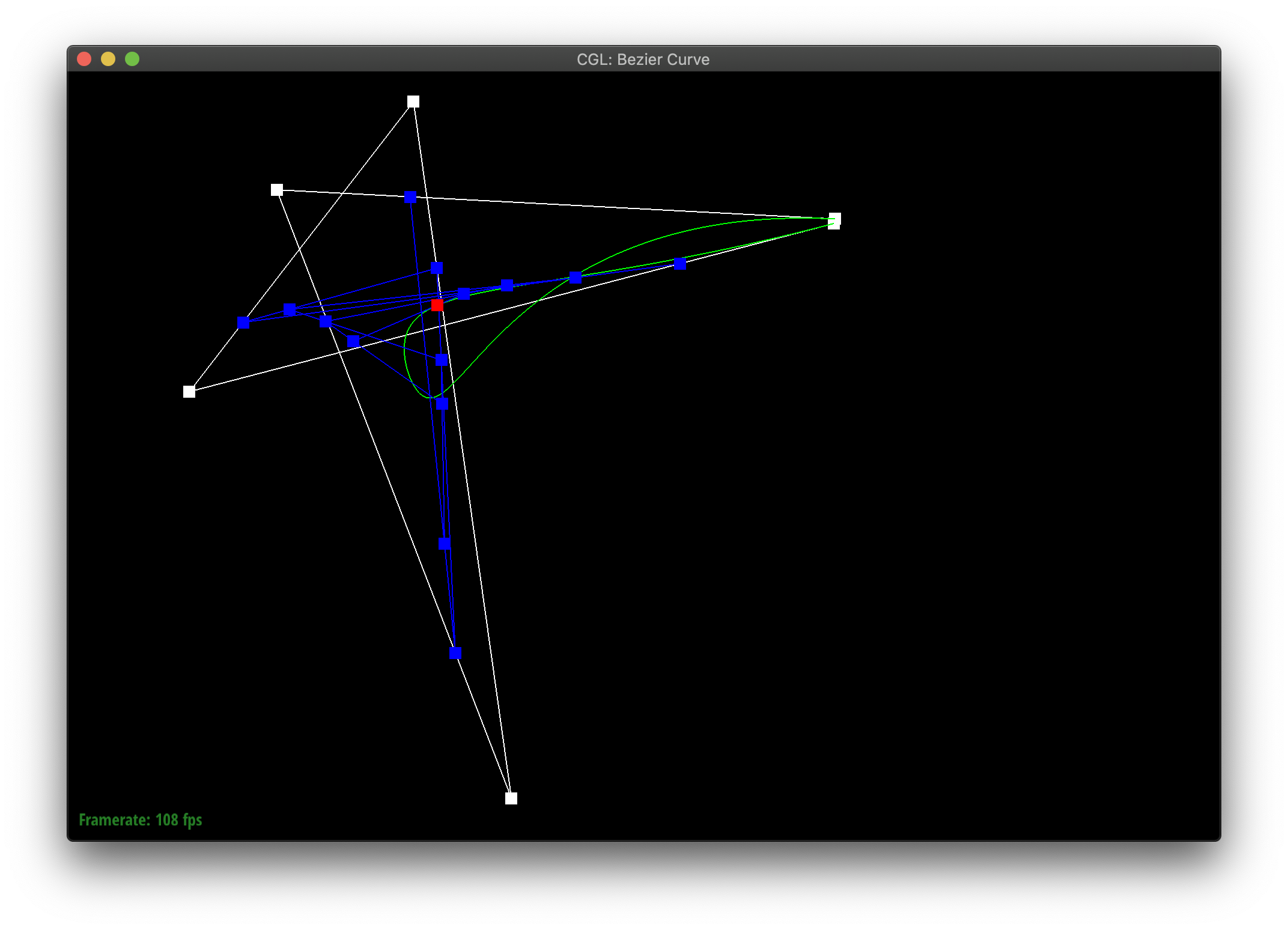
De Casteljau's algorithm allows you to define a curve between points by recursively finding interpolated midpoints until you meet at some middle point which the curve passes through. We implemented this in part 1, by showing how to reduce an iteration of the algorithm with n points to one with n-1 new points. You essentially replace the n points with the interpolation of each pair of points in order. [1, 2, 3] --> [lerp(1, 2), lerp(2,3)]

Here's my curvy creation!

Part 2: Bezier surfaces with separable 1D de Casteljau subdivision

De Casteljau's algorithm can be extended to Bezier surfaces by

• applying de Casteljau's algorithm with parameter u to each row of control points
• applying de Casteljau's algorithm with parameter v to all of the results of the previous steps

This functionally interpolates each of the 4 rows of control points using u, then interpolates the four resulting interpolated points using v to get the single interpolated point from (u,v)

Section II: Sampling

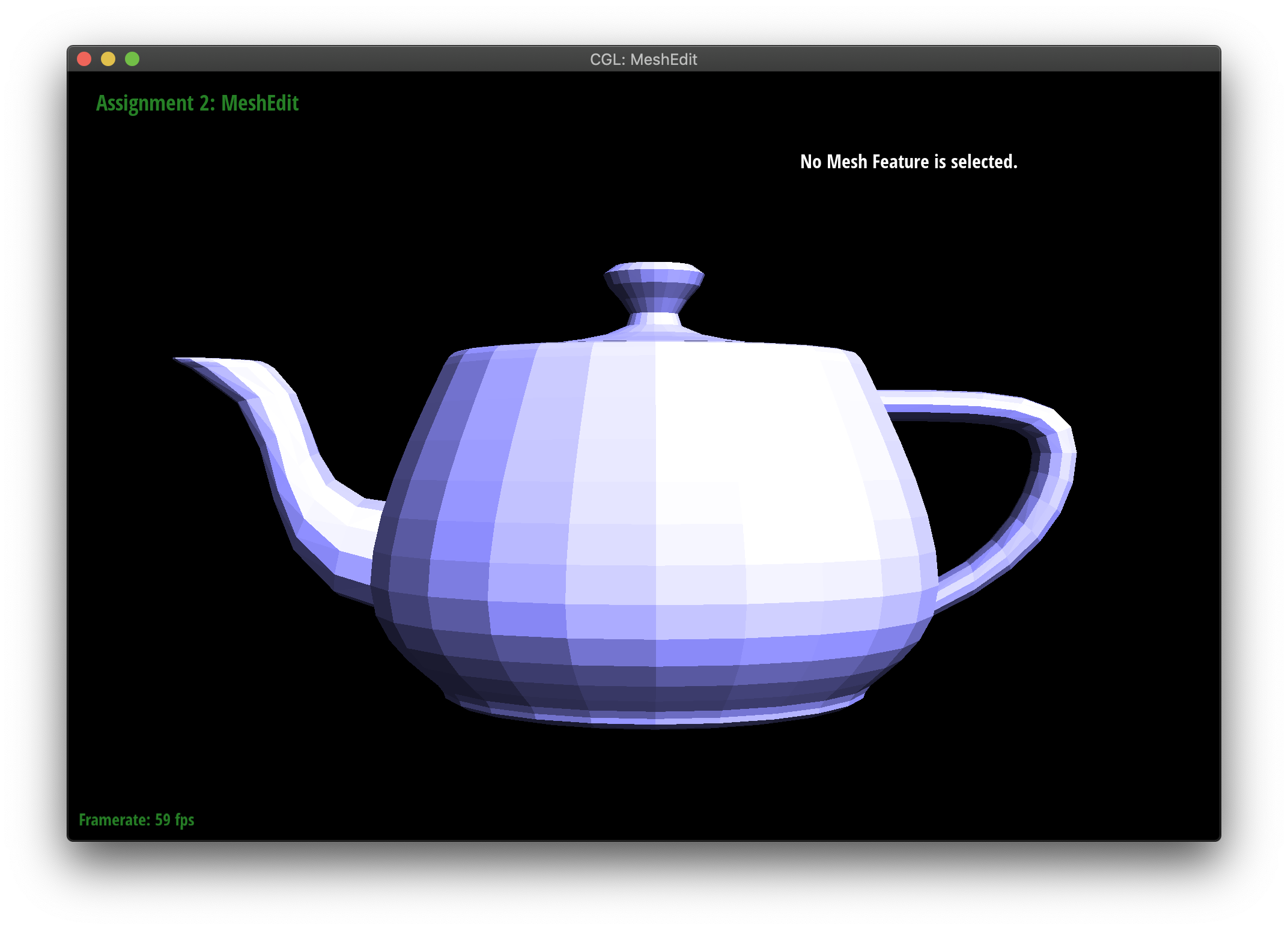
Part 3: Average normals for half-edge meshes

I iterated through each face by calling getting the next of the twin of each half-edge. For each face, I accumulated the result face's normal method, then I used the unit function to normalize that sum.

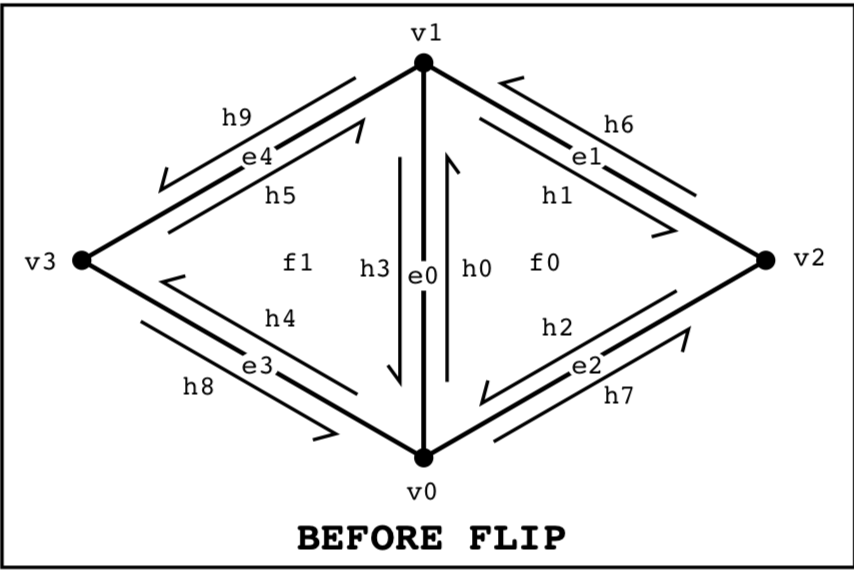
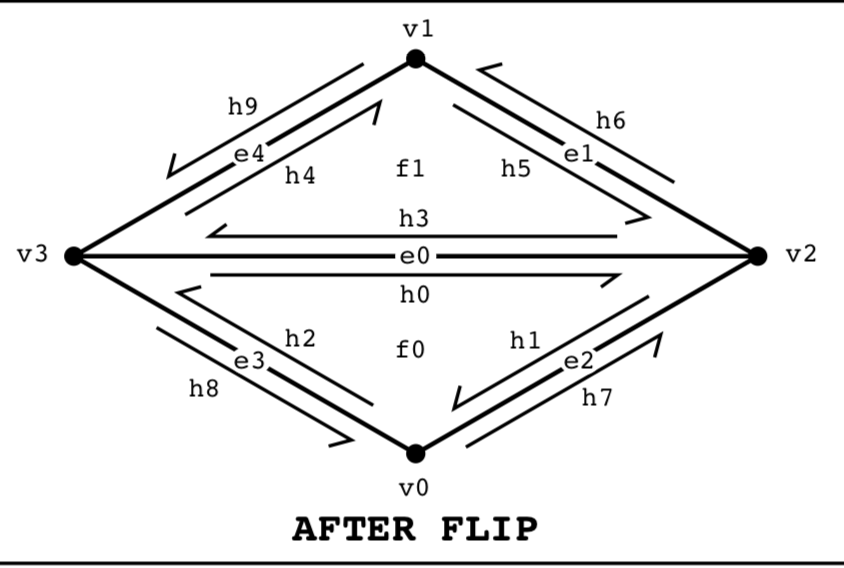
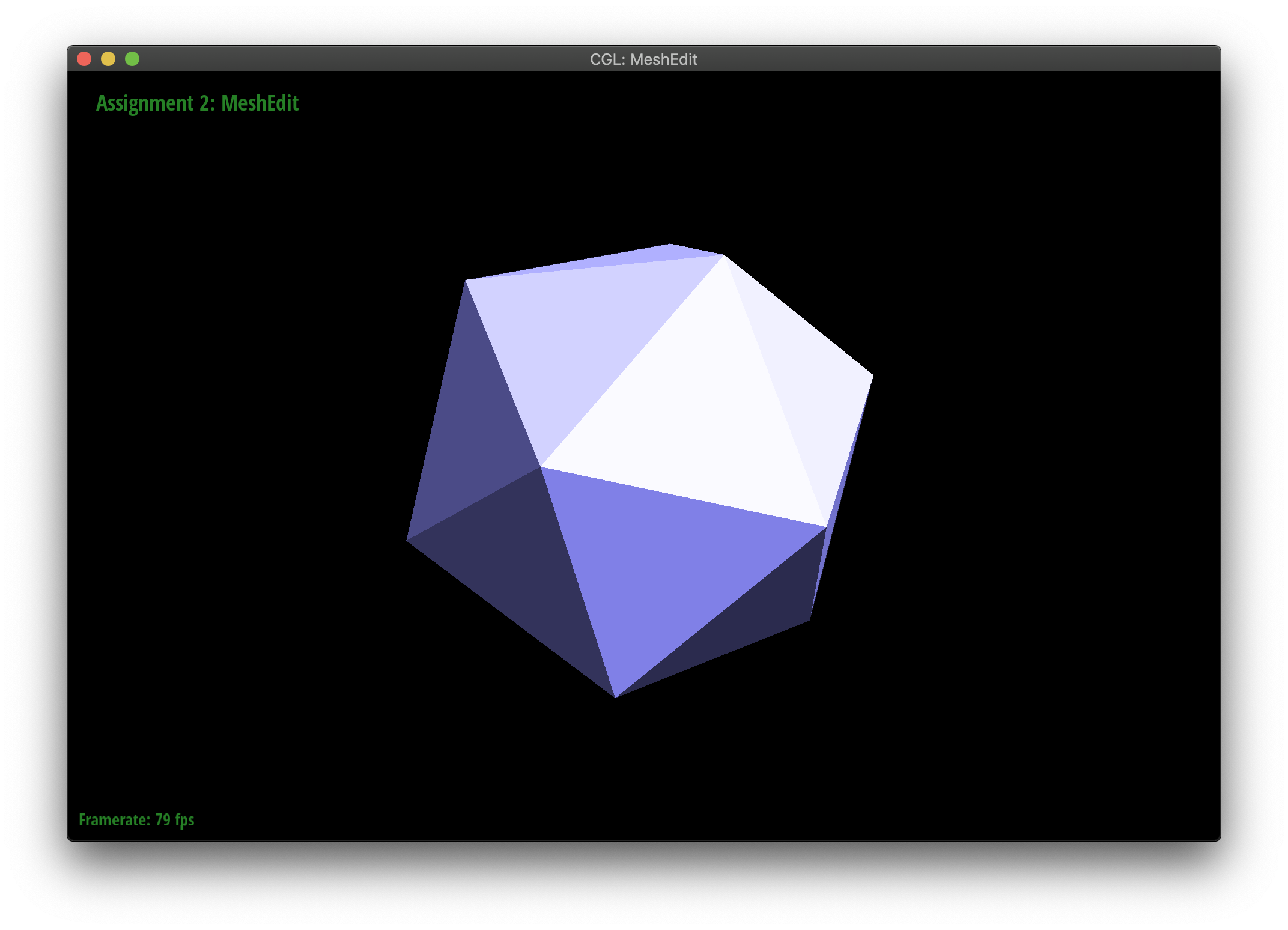
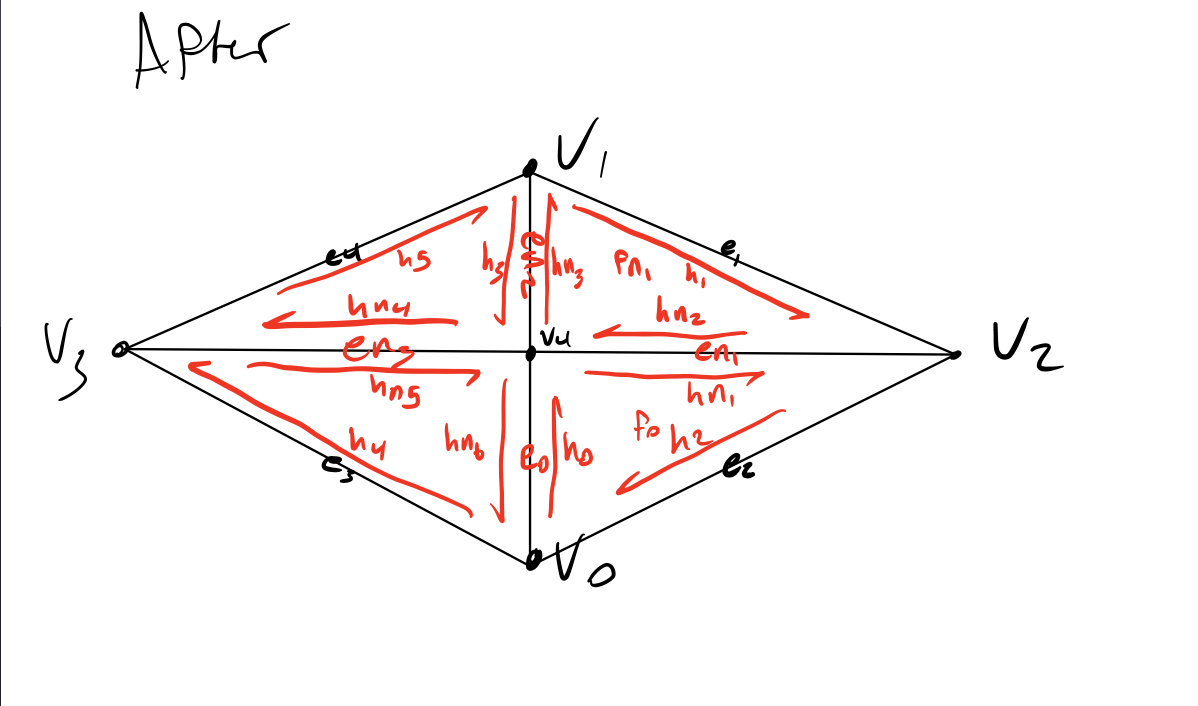
Part 4: Half-edge flip

Starting with a picture of the flip operation, it became a systematic process. I mapped each begining object to the after object, then figured out what transformations had to be applied to get it there. I began by following each half-edge and figuring out how each of it's quantities changed. Drawing pictures myself also helped. Keeping my code clean and systematic also helped a lot. It helped to think of what happened in one direction, then to think about what happened to the twins.

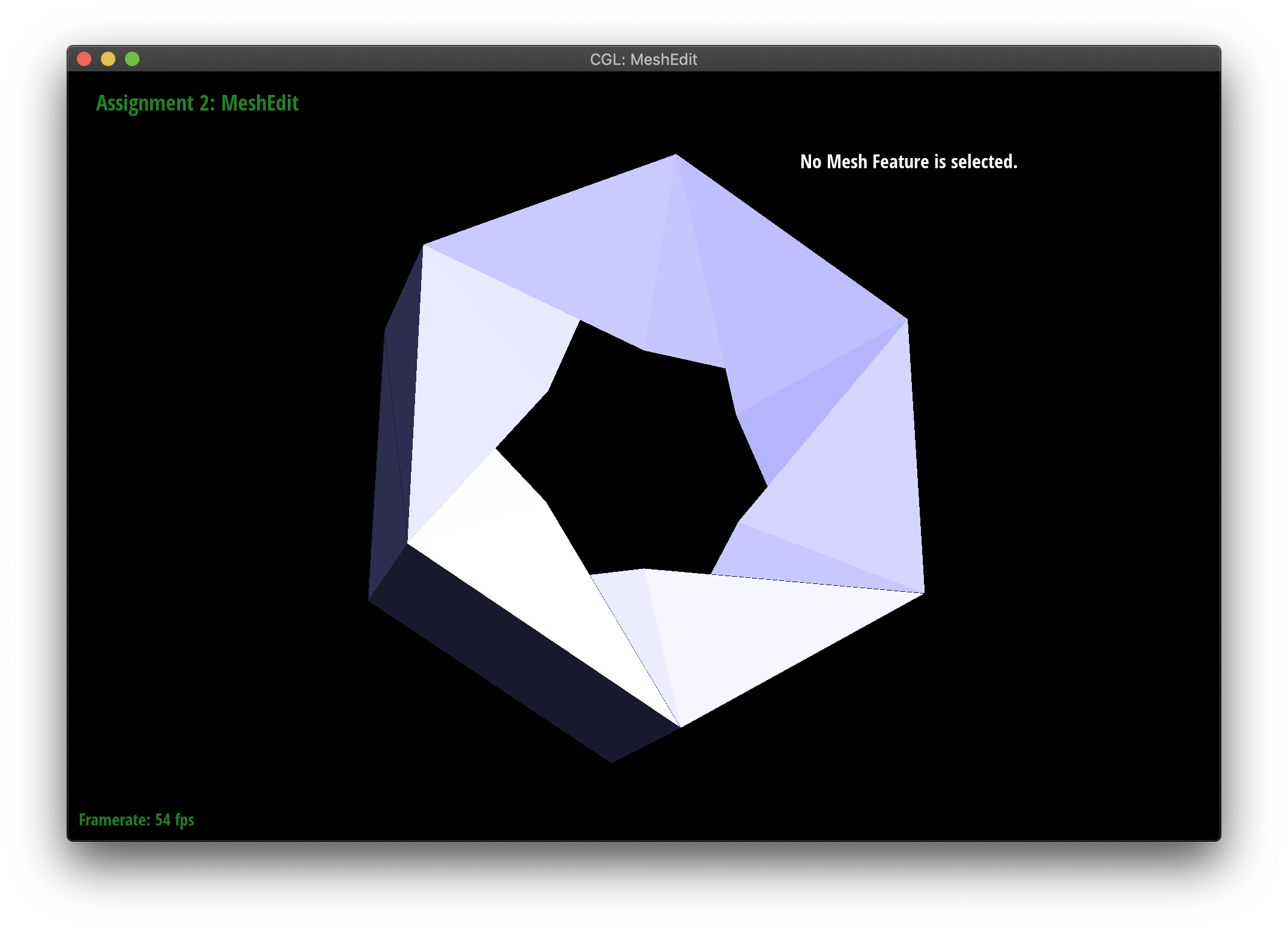
Part 5: Half-edge split

Splitting followed a similar process to flip. This time we also have to create a vertex, 6 new half-edges, 3 edges, and 2 new faces. I drew a picture and mapped each pointer to where it went in the after picture. Just like last time, thinking about what happened to the twins separately helped a lot. I've never been in a situation where keeping track of labels and pointers mattered so much:)

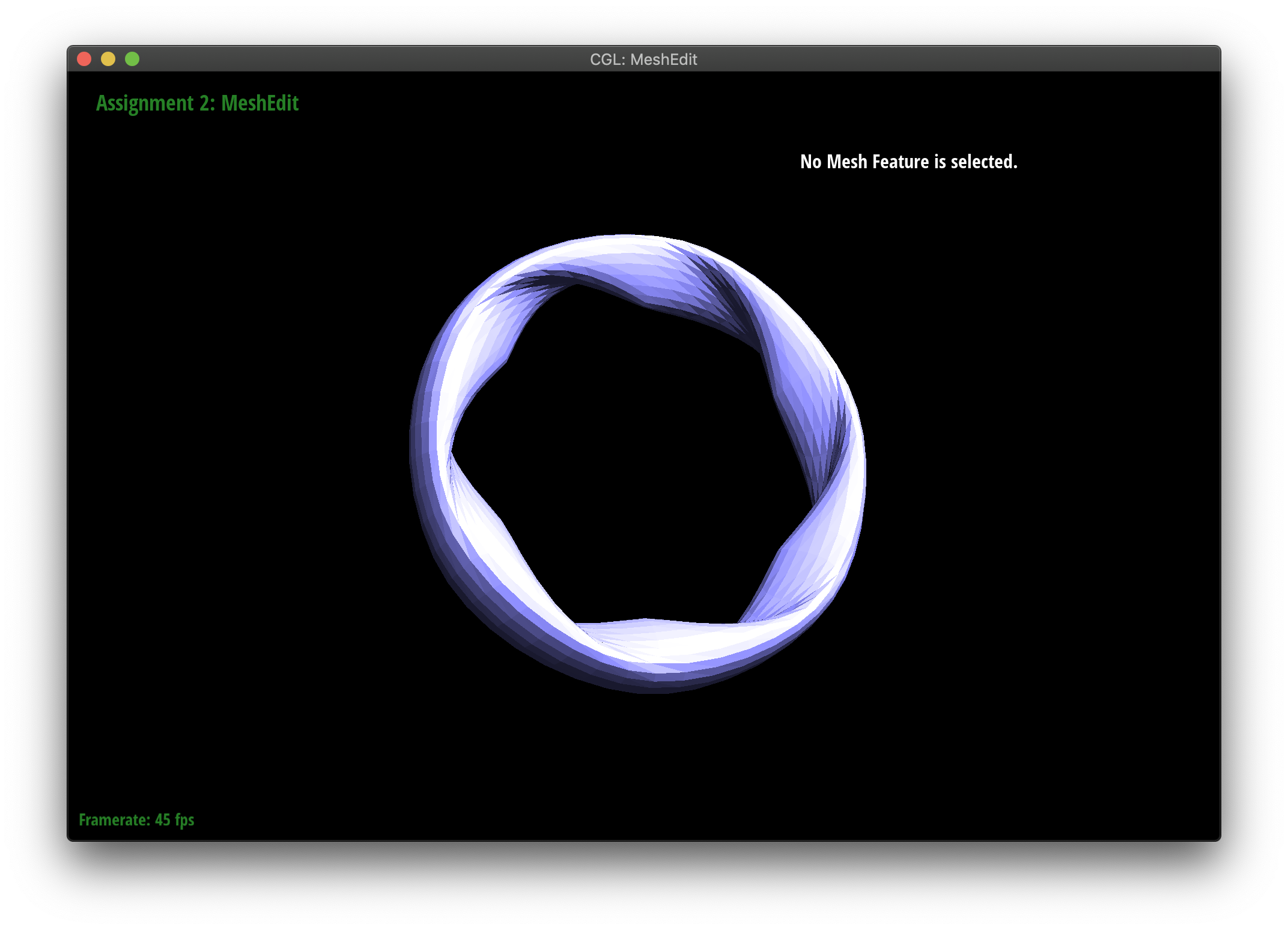
Part 6: Loop subdivision for mesh upsampling

I followed the steps in the spec. I computed new vertex and edge positions according to the formula. I figured out what the last edge was in the old ones, by doing a quick loop, then split until I saw my last_original_edge. Then I flipped the requried edges and copied over the new vertex positions.

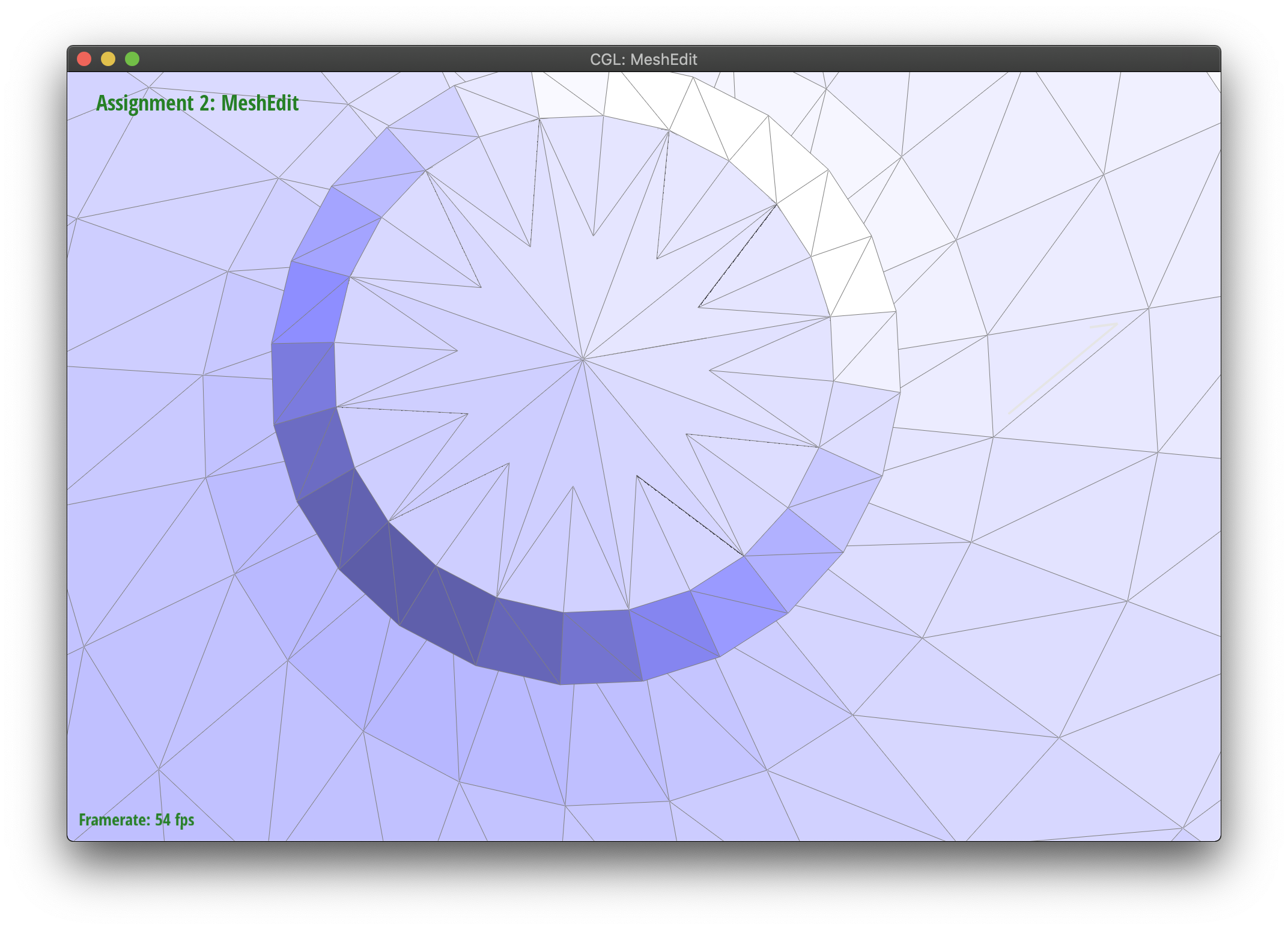
Maintaining corners by splitting

Upsampling seems to smooth out sharp corners and edges. You can lessen this effect by spliting interior edges a ton of times. Notice how the edges are maintained on the pre-split face.

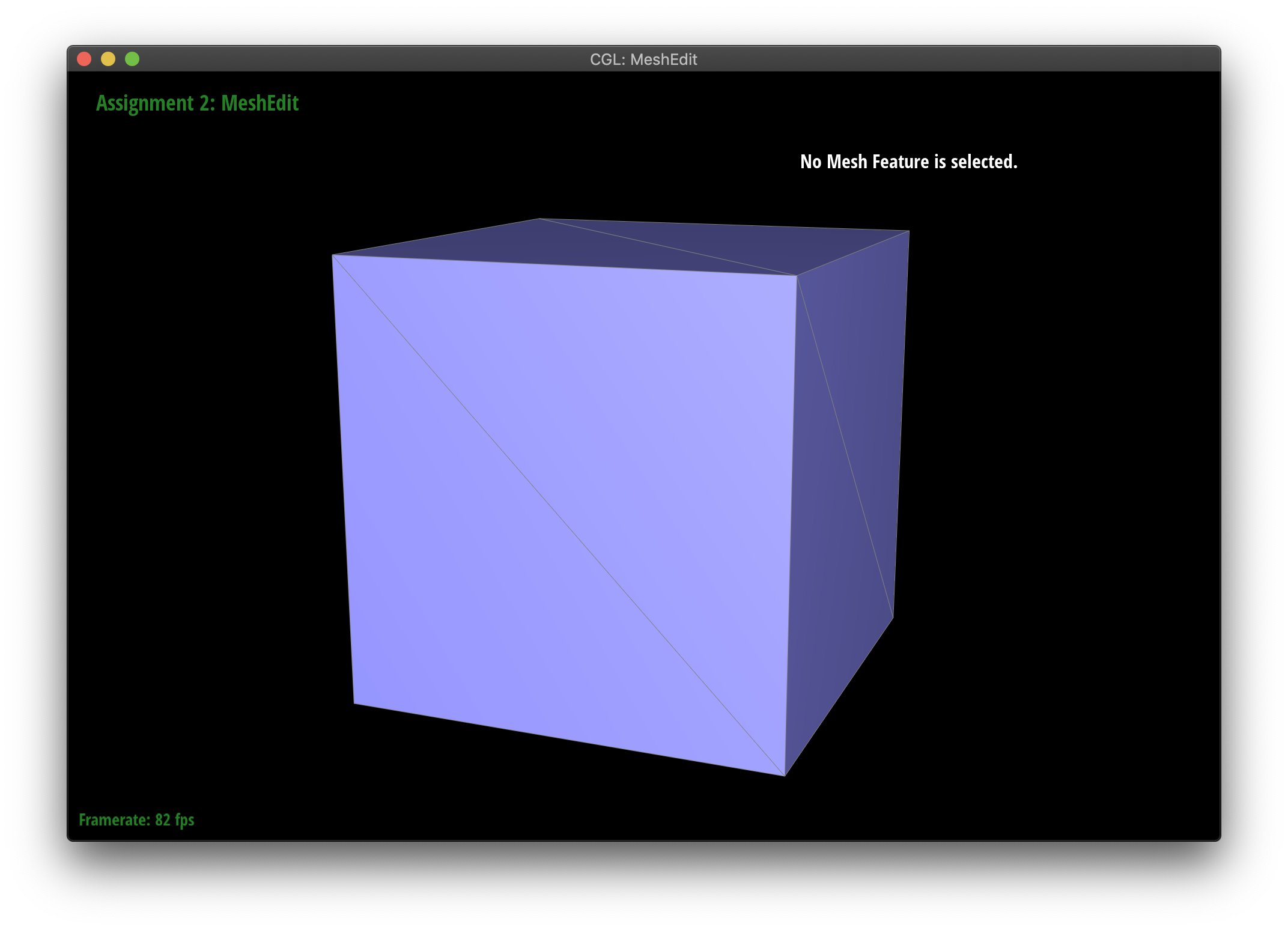
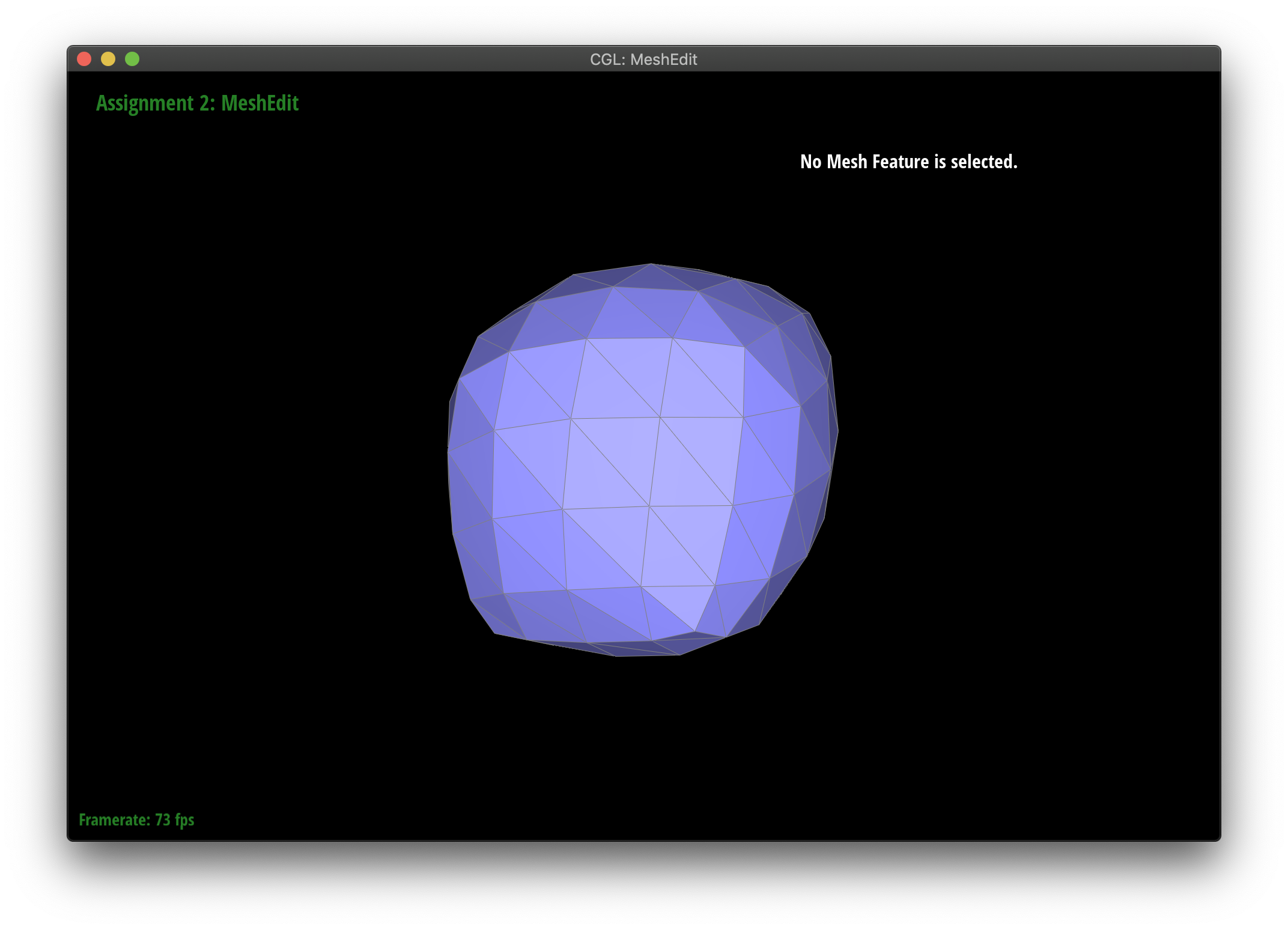
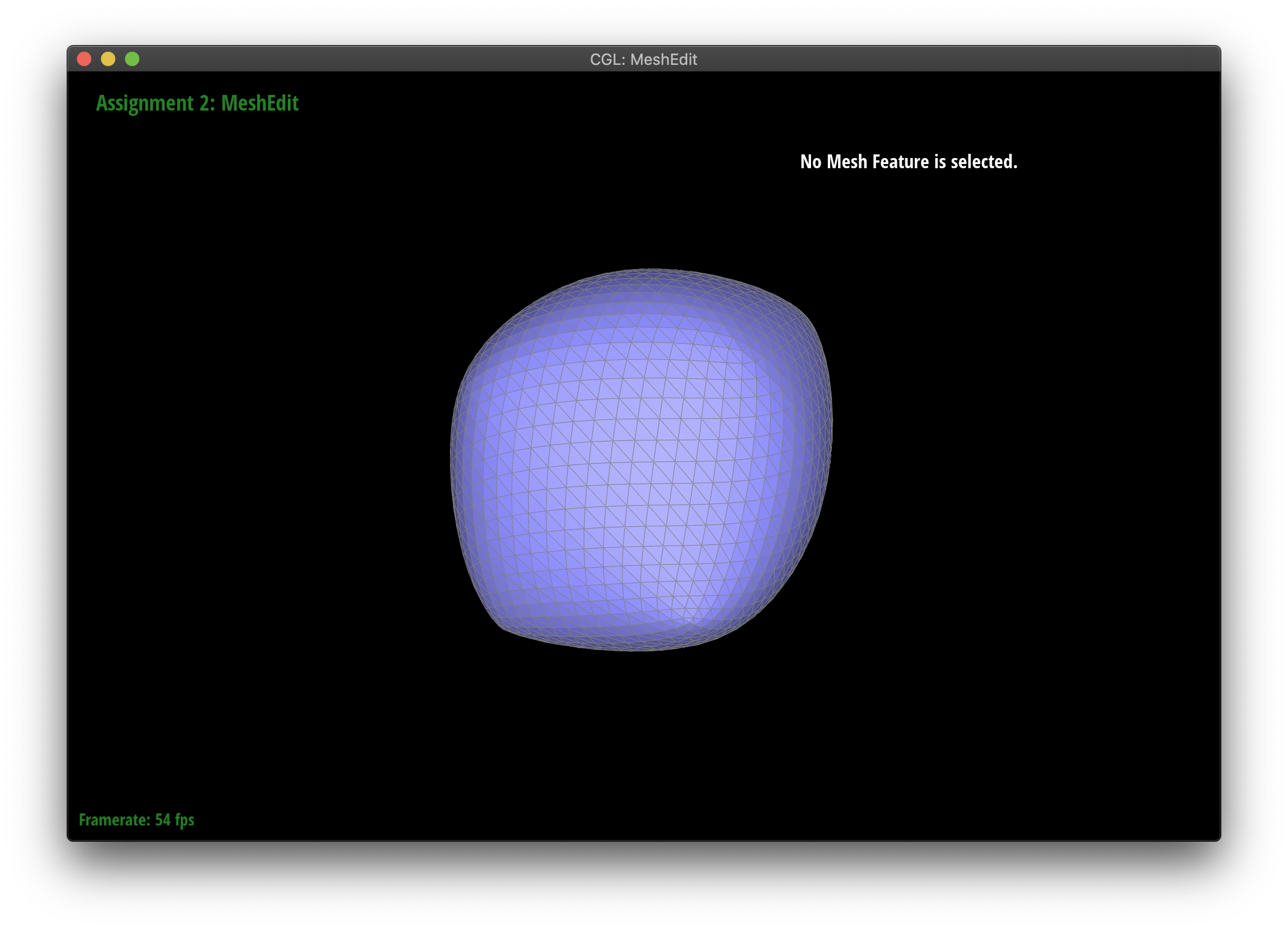
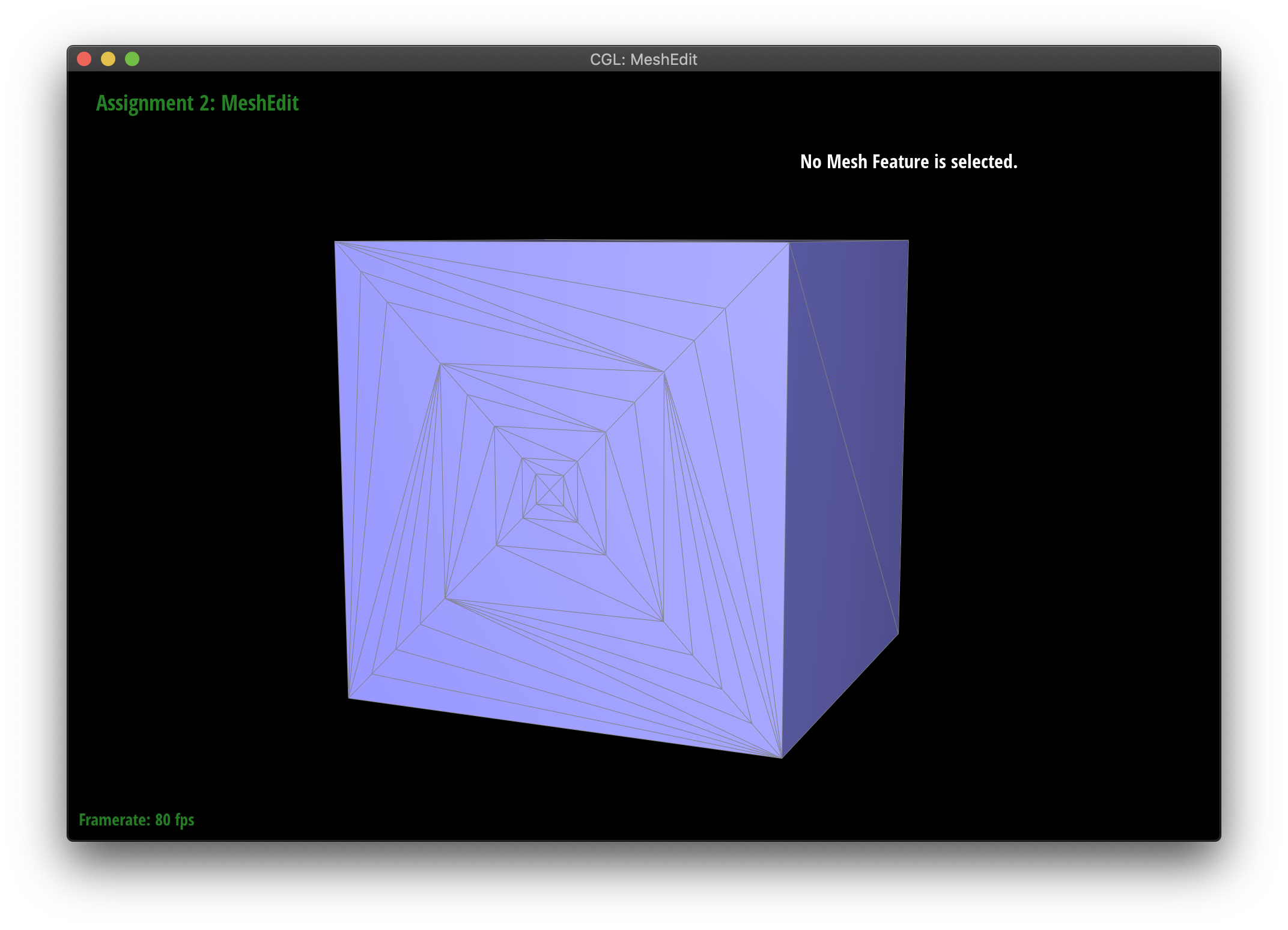
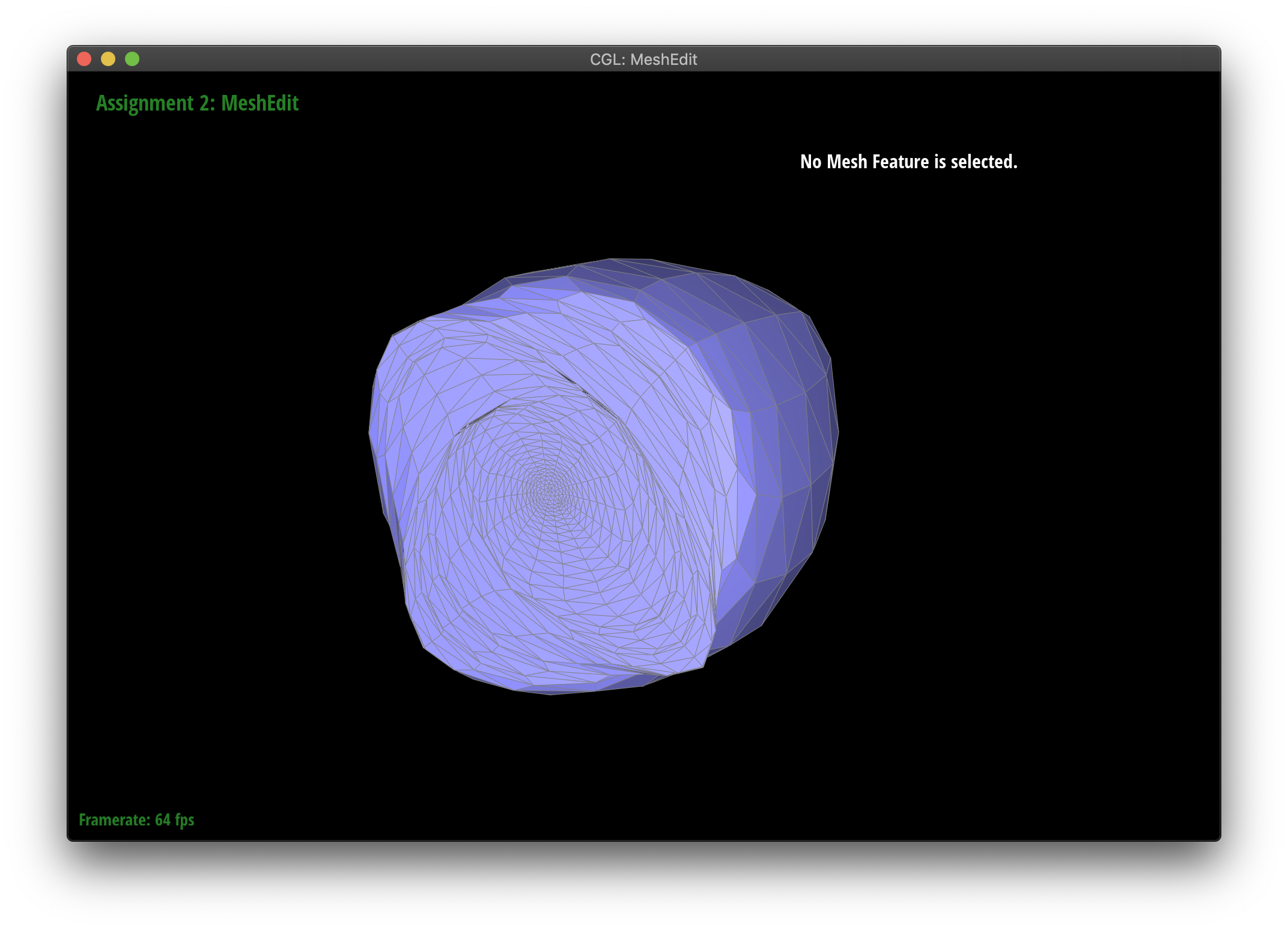
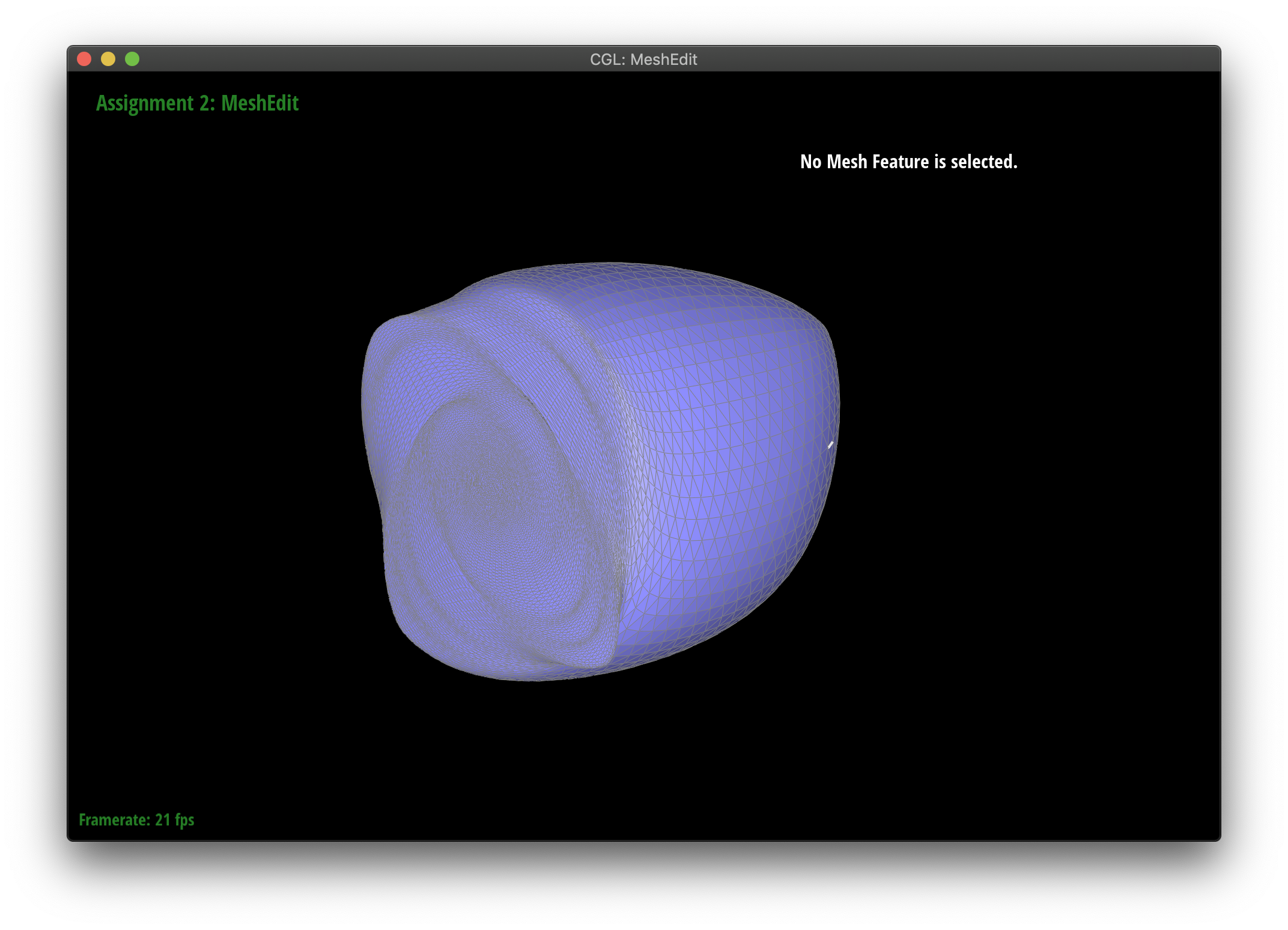
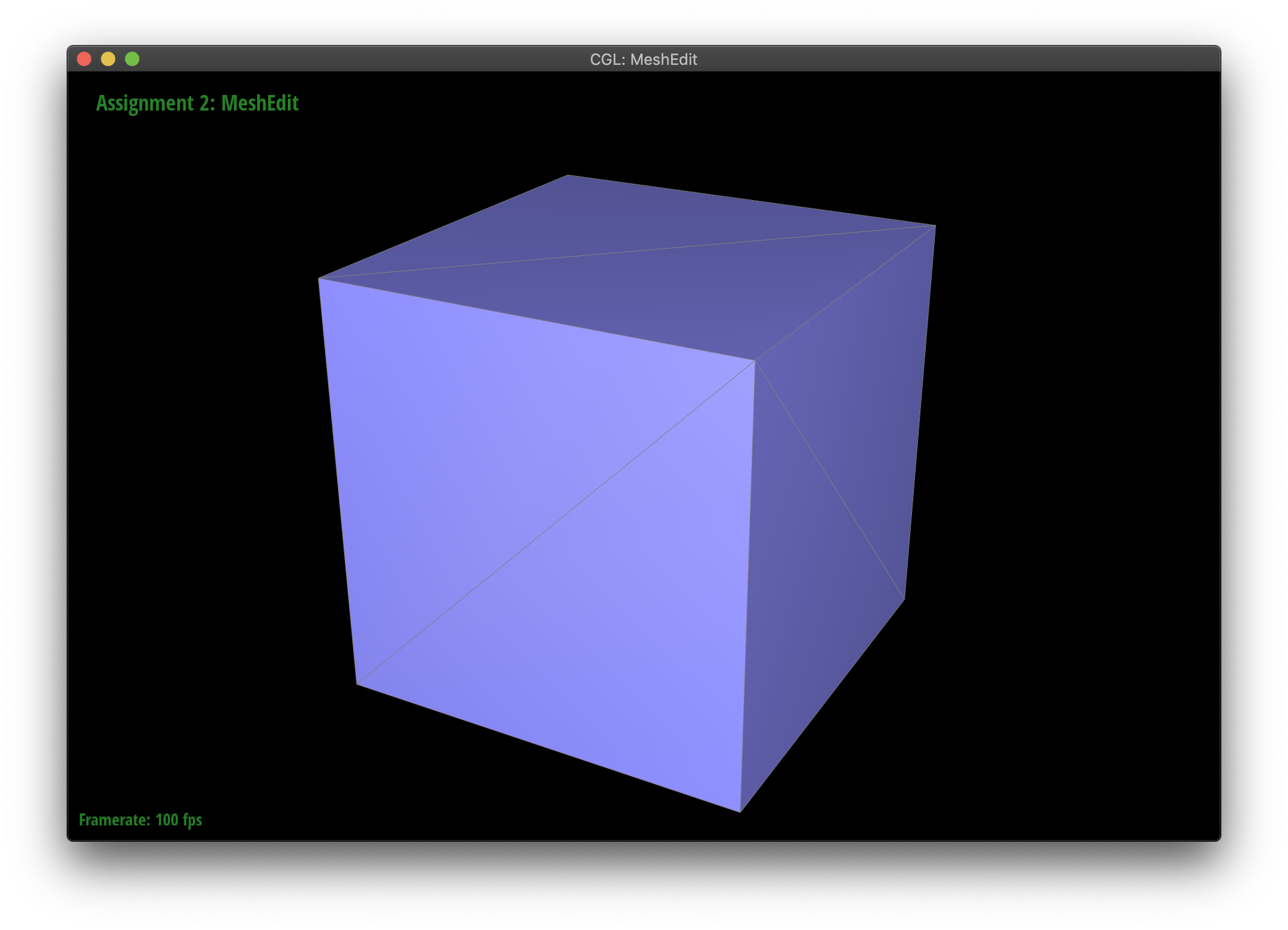
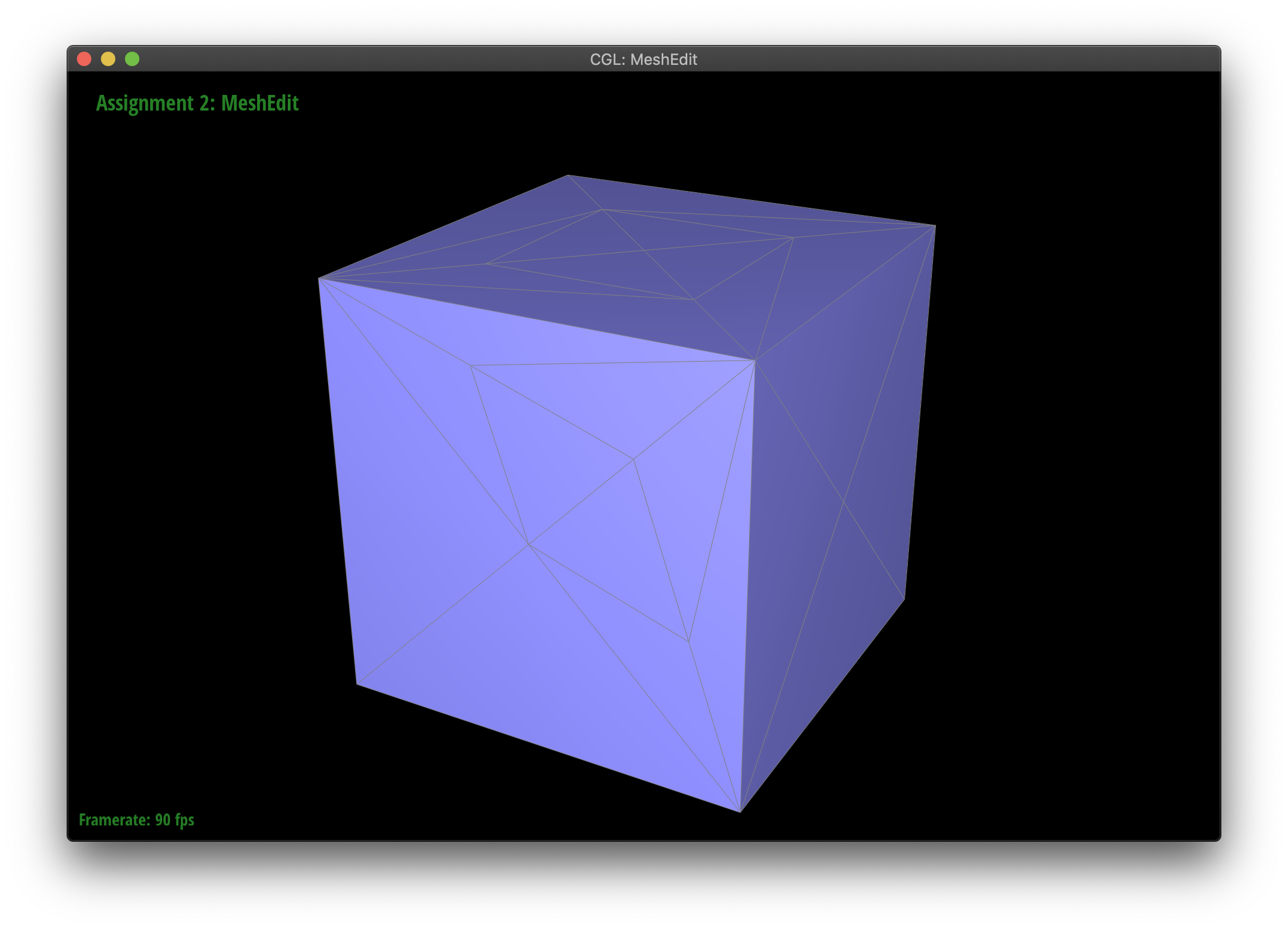
Maintaining symmetry by splitting

Upsampling causes some weird asymmetry on the cube. You can lessen this effect by spliting interior edges on all faces. Notice how the symmetry holds better. It seems that the asymetry is occuring because there is only one edge per face and each diagonal edge points in a different direction. Splitting each face makes it so that each face has identical edge layouts. That preserves the symmetry better as you upsample.
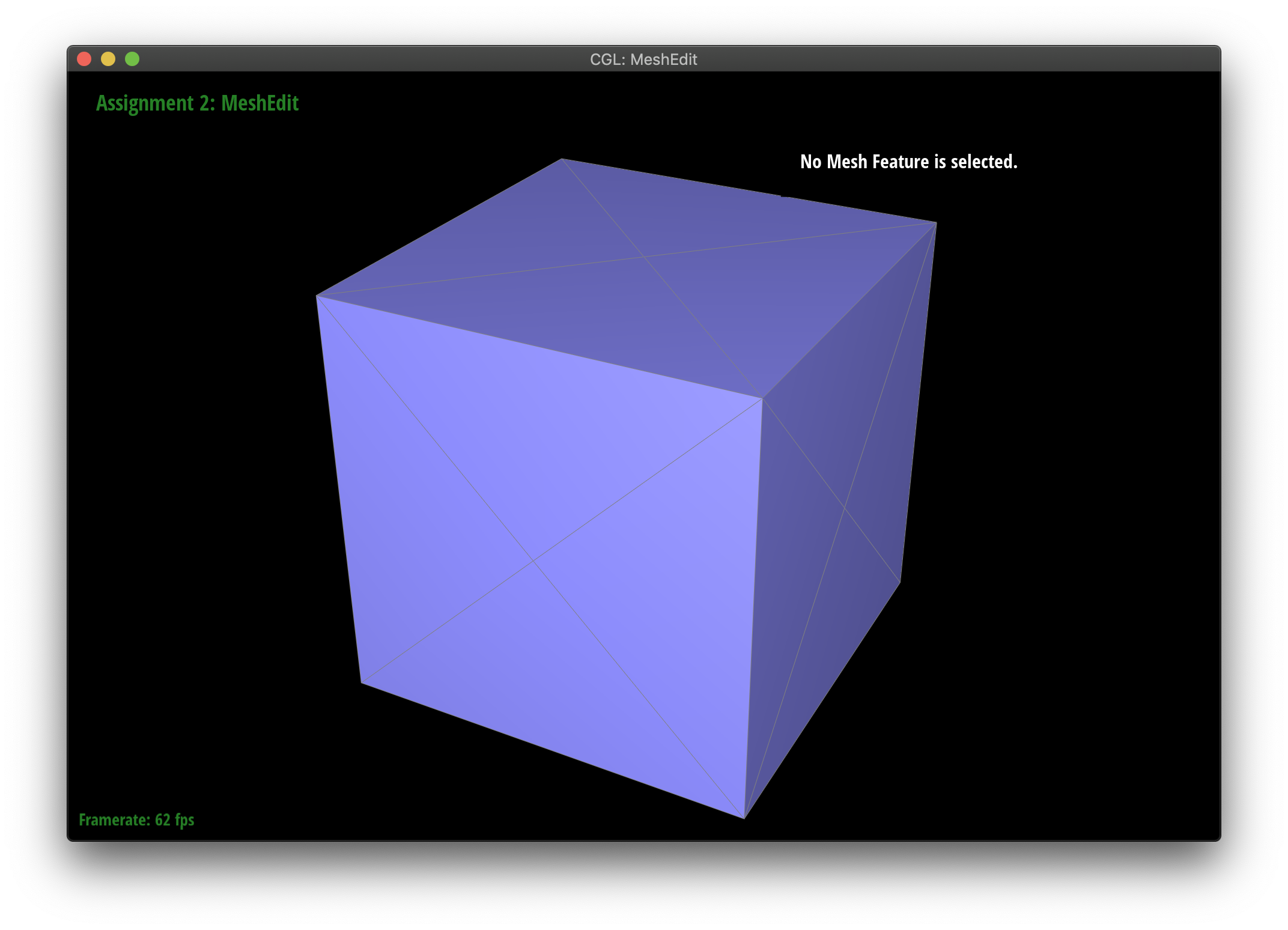
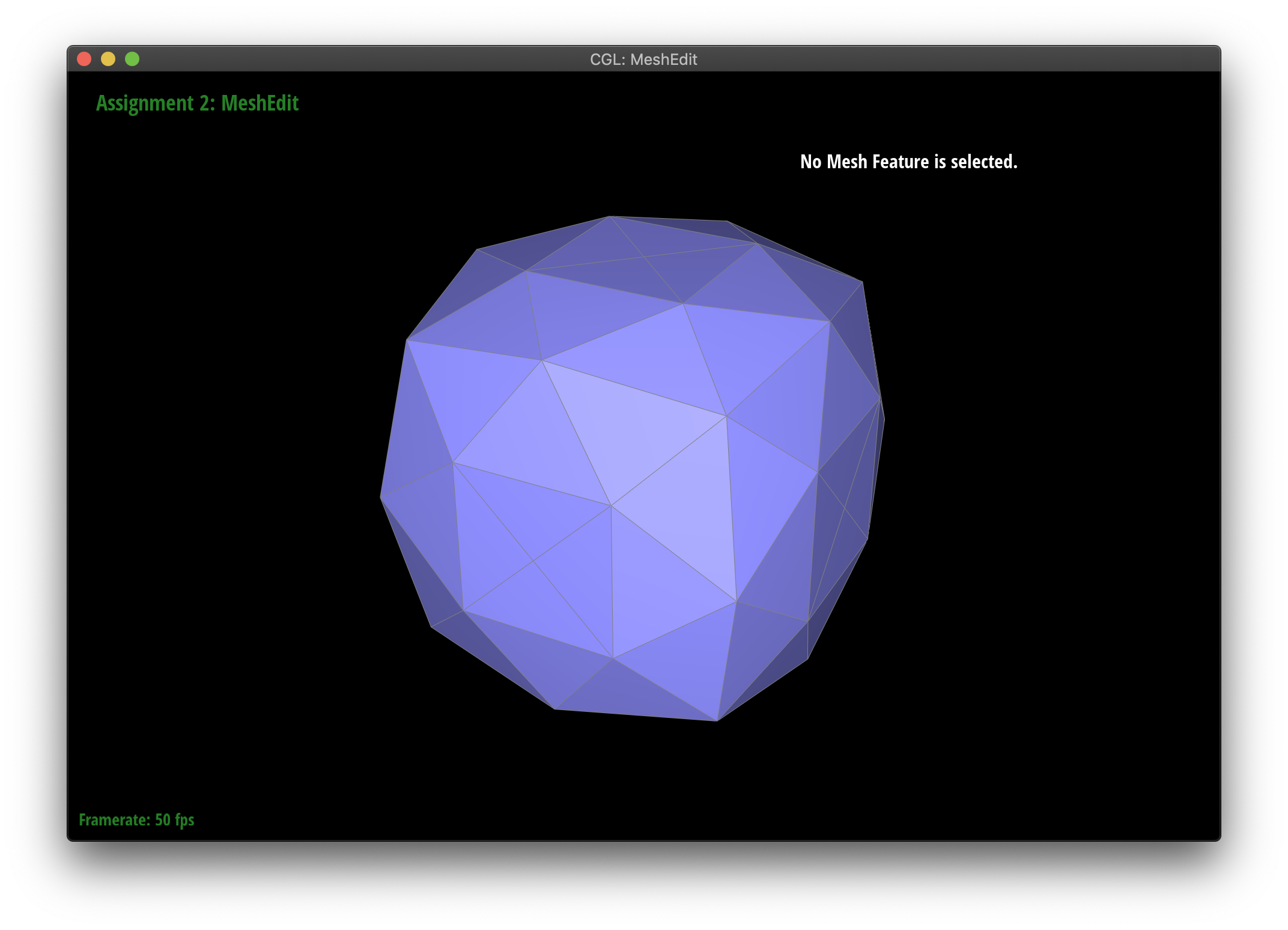